D'Hondt es el método usado en España para el reparto de escaños en cada circunscripción. Se nos suele explicar el método, pero no porqué hacemos todas esas operaciones. Una forma más visual de entender D'Hondt nos dará las claves para desmontar muchos mitos y entender el efecto real de nuestro voto.
- El procedimiento
- Un precio para un reparto exacto
- Escaños y restos
- El último cociente con escaño, \(P_{max}\)
- El primer cociente excluido, \(P_{min}\)
- Acotando y estimando el precio
- Un atajo para calcular D'Hondt
- Cociente de Hare, un mundo ideal
- La proporcionalidad o no de D'Hondt
- El poder de N votos
- Resumen
El procedimiento
Cuando se nos explica el método de D'Hondt que usamos para repartir los escaños en una circunscripción, se nos suele explicar un procedimiento, el objetivo del cual queda tras la niebla de su complejidad. No hace falta que lo descifres porque lo voy a simplificar abajo, pero sería:
Para cada candidatura X, se calcula el cociente \(V_X \over S_X + 1\) donde \(V_X\) son los votos obtenidos por esa candidatura y \(S_X\) los escaños que le han sido repartidos hasta el momento, inicialmente 0. Se asigna escaño a la candidatura con el cociente más alto, se le recalcula su cociente y se repite hasta que todos los escaños se han repartido.
Parte de la complejidad viene de que se intenta minimizar los coeficientes (divisiones) a calcular, lo que es de agradecer si tenemos que hacerlo a mano. Pero, hoy en día, tenemos ordenadores. Al final lo que estamos haciendo es:
Otorgar escaño a los mayores cocientes resultantes de dividir los votos de cada candidatura por sucesivos enteros 1, 2, 3...
Lo que se muestra en esta tabla del simulador:
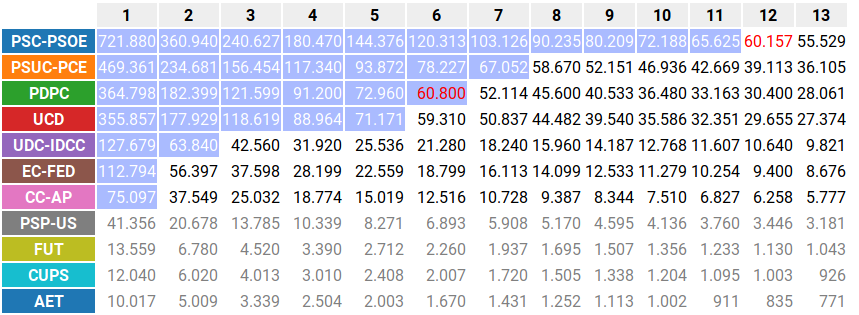
Aunque sigue sin estar explícito, con esta simplificación, es posible que ya intuyas por donde va la cosa.
- ¿Qué significan estos cocientes?
- ¿Porqué escogemos los más altos?
Vamos a ello.
Un precio para un reparto exacto
El método de D'Hondt resuelve el problema de encontrar un precio (cuántos votos ha de costar un escaño) para que se repartan exactamente los escaños disponibles, ni de más ni de menos.
¿Cuál ha de ser el precio para que una formación obtenga N votos? Por ejemplo, una candidatura que tenga 100.000 votos:
- No obtendrá escaño si el precio es superior a 100.000
- Obtendrá un escaño cuando sea 100.000 (100.000/1) o menor
- Obtendrá dos cuando sea 50.000 (100.000/2) o menor
- Obtendra tres cuando sea 33.333 (100.000/3) o menor
- ...en general, podrà obtener N escaños cuando el precio sea 100.000/N o menor
Eso es lo que representan los cocientes: el precio máximo por el que cada candidatura puede obtener un cierto número de escaños.
¿Y porqué escogemos los cocientes ordenados de mayor a menor? Es una forma de bajar el precio de forma controlada, si están ordenados cada cociente añade un escaño y solo uno a los ya seleccionados, asegurando el reparto exacto cuando tengamos tantos cocientes como el número de escaños disponibles.
Esta es la perspectiva del método de D'Hondt que nos va a permitir llegar a un montón de conclusiones sobre como funciona el sistema electoral. Así que vamos a escarbar un poco más.
Escaños y restos
Una vez establecido un precio, los votos que ha recibido una candidatura pueden servir para sumar escaños, o, si no llegan, a formar parte de los restos. Esto es importante porque muchas de las cuestiones a resolver tienen que ver con esos restos, cómo se nutren para obtener el siguiente escaño o cómo se agotan para perderlo.

Esta captura del simulador visualiza como, dado un precio, los votos de cada candidatura se reparten en tantos segmentos, del tamaño del precio, como escaños se consiguen. La parte translúcida del final son los restos que no han llegado al siguiente escaño.
Cuando un precio consigue que los escaños repartidos coincidan con los disponibles, tenemos un reparto exacto.
Más formalmente, D'Hondt nos sirve para encontrar un precio, \(P\), tal que, para cualquier candidatura X:
Donde:
- \(V_X \in \mathbb{N}\) son los votos que ha obtenido X, tal que \(V_{total} = \sum_{\forall X}{V_X}\)
- \(S_X \in \mathbb{N}\) son los escaños que consigue X del reparto, tal que \( S_{total} = \sum_{\forall X}{S_X}\)
- \(R_X \in \mathbb{R}\) son los restos que sobran de repartir a \(P\) y se tiene que dar que \( 0 <= R_X < P\)
El último cociente con escaño, \(P_{max}\)
El simulador marca los cocientes que han conseguido escaño con fondo azul. El último en conseguirlo, el menor de ellos, se marca con los números en rojo. Este último cociente es el que marca el precio.
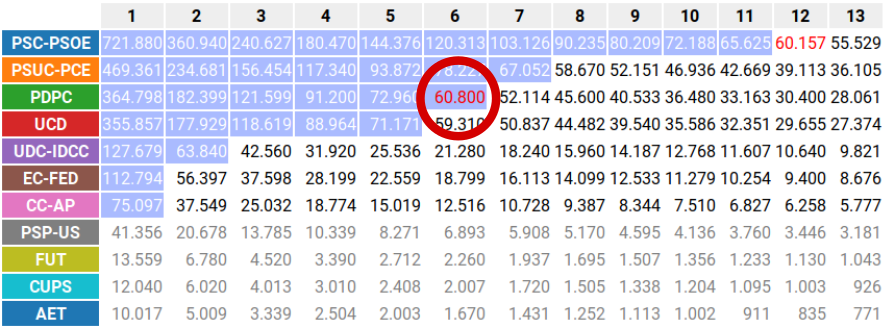
Llamemos C a la candidatura que ha obtenido este último escaño. Su último cociente escogido, \(P_C\), fijará el precio \(P_{max}\), que será el máximo con el que la candidatura C obtiene exactamente \(S_C\) escaños sin que le sobren votos.
Si el preció fuera levemente superior, C no tendría suficientes votos para obtener \(S_C\) escaños. Al reparto le sobraría un escaño y ya no sería exacto.
El primer cociente excluido, \(P_{min}\)
El simulador, deja con el fondo blanco los cocientes que no obtienen escaño. El mayor de ellos, el inmediatamente inferior a \(P_{max}\), se marca en rojo porque es el límite inferior \(P_{min}\) para los precios que resultan en un reparto exacto de los escaños. De ese precio para abajo, se reparten escaños de más. Resulta en un reparto exacto cualquier precio \(P\) en el intervalo:

Llamemos D a la candidatura a la que pertenece y, al coeficiente, \(P_D\). Si dicha candidatura, a precio \(P_{max}\), obtenía \(S_D\) escaños, bajando el precio a dicho coeficiente, obtendría \(S_D +1\) escaños y estaríamos repartiendo uno de más.
La existencia de estos dos precios, \(P_{min}\) y \(P_{max}\), y sus dinámicas nos servirán, en otros artículos, por ejemplo, para simplificar bastante el análisis de los efectos de un trasvase de votos entre candidaturas, limitando la influencia de las muchas candidaturas a la existencia de estos dos coeficientes. Ya lo veremos.
Acotando y estimando el precio
Ahora que conocemos que el objetivo de D'Hondt es encontrar un precio que reparta los escaños exactamente, podemos experimentar con otras formas de encontrarlo.
Por ejemplo, podemos empezar por un precio arbitrario, si sobran escaños bajamos el precio, si faltan lo subimos, hasta que encontremos un precio que reparta exactamente los escaños, uno entre \(P_{min}\) y \(P_{max}\).
En una búsqueda como esta, es muy útil acotar los precios posibles. Usemos estos dos casos extremos:
El mayor precio posible se da cuando todos los votos a candidaturas sirven para obtener escaño y no hay restos1. Este precio también se llama cociente de Hare, y hablaremos más sobre él:
El menor precio se daría si las \(K\) candidaturas se quedasen al límite del obtener el siguiente escaño y sus restos fuesen casi el precio del escaño2:
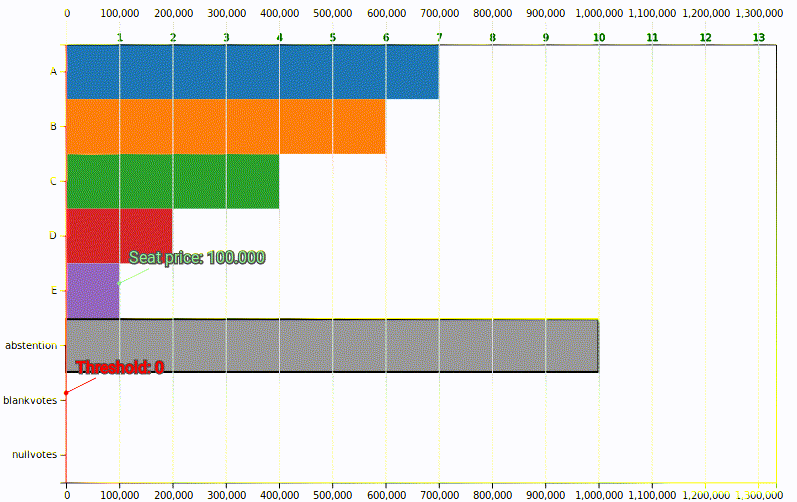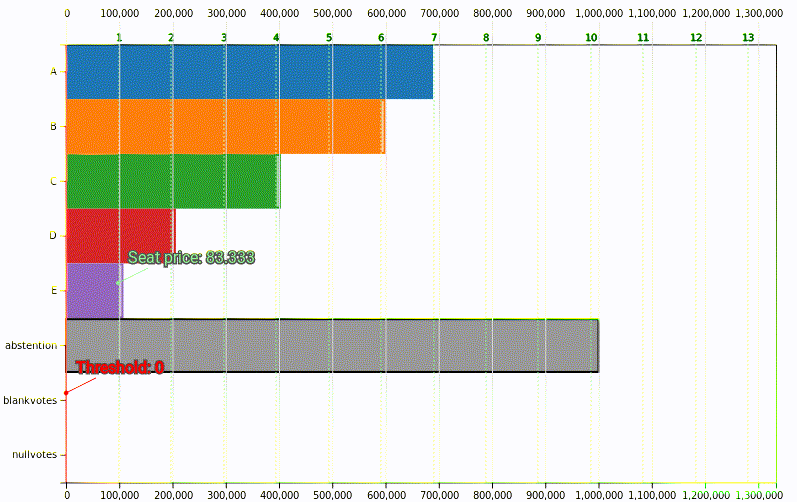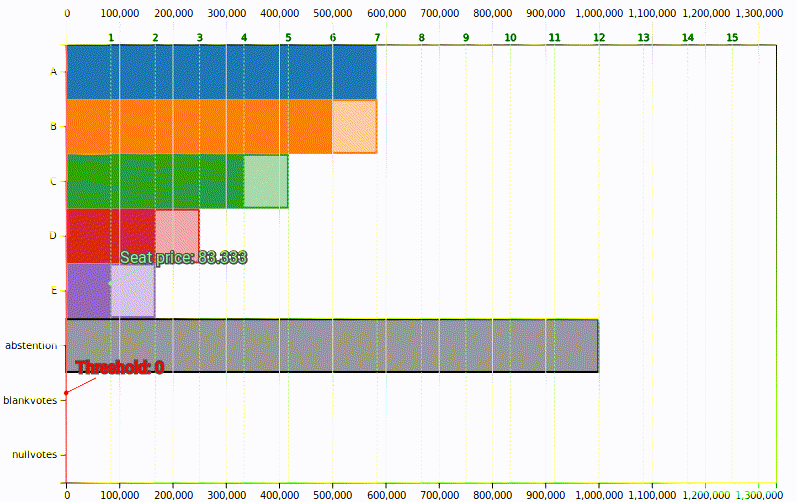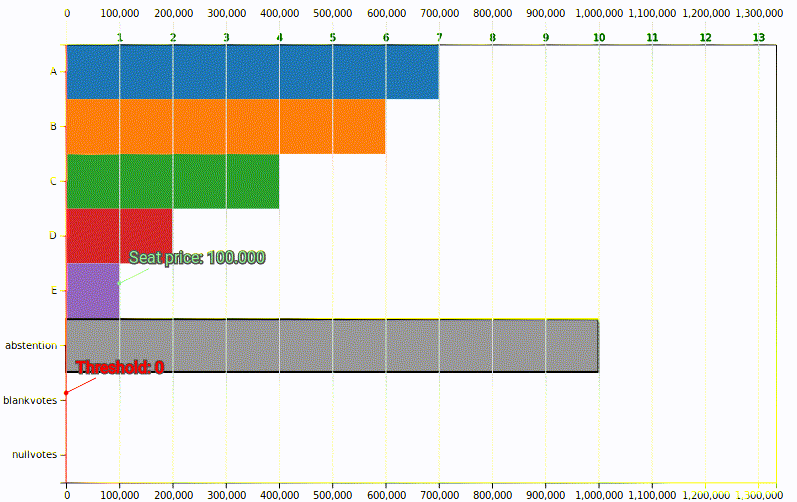
Con los mismos votos a candidaturas (2M), el precio variará según los votos que vayan a restos.
Esto nos deja el siguiente panorama:
Suponiendo que las candidaturas con opciones a representación (\(K'\)), por ejemplo, aquellas que superen \(P_L\), se quedarán en media a la mitad entre un escaño y el otro, también podemos ajustar un buen precio de partida para la búsqueda3:
Estas cotas y estimaciones del precio del escaño no sólo sirven para hacer este tipo de búsqueda. También son útiles para nuestra cruzada contra los mitos electorales.
Por ejemplo, para evaluar el efecto del umbral electoral. Si una circumscripción reparte 4 escaños y hay 5 candidaturas en liza un precio de entre el 25% y el 10% limita mas que un umbral al 3% o al 5%. En las pocas circumscripciones y convocatorias que si afecta, nos puede servir para evaluar si es mejor desistir o apoyar una candidatura que puede quedar lejos o cerca de obtener varios escaños de golpe o ninguno.
De forma similar, también son útiles para determinar, por ejemplo, la masa crítica de un voto estratégico coordinado.
Un atajo para calcular D'Hondt
Como sabemos que el precio de D'Hondt será igual o menor que \(P_{Hare}\), ¿por qué no empezar a calcular cocientes a partir de ese punto?
- Calculamos el cociente Hare \(P_{Hare} = V_{total} / S_{total}\)
- Dividimos los votos de cada candidatura por dicho precio
- Asignamos los escaños determinados por la parte entera resultante
- Calculamos los coeficientes para el siguente escaño de cada candidatura
- A partir de ahí aplicamos D'Hondt: asignamos escaño al mayor coeficiente, recalculamos coeficiente y vuelta a empezar hasta que no queden escaños.
Es un método más eficiente si se da la condición de que haya más escaños a repartir que candidaturas con opción a escaño.
Cociente de Hare, un mundo ideal
Imaginad un "mundo ideal" en el que se pudiera descuartizar candidatos y obtener, por ejemplo, 5'61 escaños. Motosierra en mano, podríamos conseguir representaciones exactamente proporcionales al número de votos.

Aquí ya han conseguido ser proporcionales.
El precio a pagar por escaño en este "mundo ideal", a parte de la sangre, es el cociente de Hare. Sí, la cota superior que habíamos establecido antes para el precio de D'Hondt.
Por desgracia, este tipo de descuartizamiento es ilegal en la mayoría de democracias. Nos tendremos que quedar, como mucho, con la parte entera. Pero, después, quedarían por repartir los escaños que quedaban fraccionados. En esto es en lo que difieren distintos métodos de reparto llamados proporcionales.
Si quisieramos alejarnos lo menos posible de la proporcionalidad de Hare, una buena opción sería darle un escaño extra a las candidaturas con mayores restos, las que estarían más cerca de obtener el siguiente escaño. Esto sería el Método Hamilton o de mayores restos. También tiene una cierta divergencia con el reparto sádico/ideal de Hare, pero intenta ser justo en la distribución de los escaños fraccionados, minimizando la sobre/infa-representación.
El origen de la desproporcionalidad está vinculado, pues, a los escaños fraccionados de Hare. Contra más escaños enteros se repartan, más proporcional será el resultado. Los escaños fraccionados están acotados entre \(0\) y \(K\) se pueden estimar como la mitad de las candidaturas con opción \(K'/2\).
La proporcionalidad o no de D'Hondt
D'Hondt consiste en bajar el precio hasta que se repartan todos los escaños. Como el coeficiente de Hare es la cota superior para dicho precio, esto asegura que los escaños enteros de Hare se repartirán igual, garantizando un cierto nivel de proporcionalidad. La desproporción, otra vez, vendrá en como se repartirán los escaños fraccionados.
Partimos de los restos de Hare, como en Hamilton, por eso podemos decir que D'Hondt también favorece a las candidaturas que se habían quedado cerca del escaño. Pero no es el único criterio. Al bajar el precio, los restos de cada candidatura se van a nutrir con lo que ahora le sobrará a cada escaño ya obtenido.
Por ejemplo, si el precio se reduciera 3 votos, una candidatura sin escaños estará 3 votos más cerca del siguiente escaño. Pero para una candidatura con 5 escaños, 3 votos de cada uno de esos 5 escaños, ahora sobran y pasan a los restos, por lo que estará 18 votos más cerca del siguiente escaño.
Esta ventaja de los grandes para conseguir escaño es la que consigue la proporcionalidad hasta que llegamos a Hare. Pero a partir de Hare, se pasa y empieza a generar desproporcionalidad.
Este beneficio es relativo. Se nota cuando
- hay pocos escaños a repartir relativamente a las candidatura con opciones (y por tanto, menos escaños enteros de Hare respecto a los fraccionados)
- o cuando la desproporción entre candidaturas es notable y la ventaja es más significativa
Al final el gran disruptor de la proporción en el sistema electoral es la división en circunscripciones, que multiplica las desproporciones que existan en cada circunscripción.
Un método Hamilton tiene menor desproporción pero también la tiene. Esa desproporción también se vería multiplicada por la división en circunscripciones,
Y el segundo disruptor de la proporcionalidad, por delante de D'Hondt, son las circunscripciones pequeñas con pocos escaños. Es como pintar imágenes con 4 pixeles. Uses el método que uses no tienes precisión suficiente para representar la realidad.
El poder de N votos
Entonces parece que D'Hondt favorece a las candidaturas grandes. ¿Quiere eso decir que si voto a las grandes tengo más capacidad de cambio que si voto a pequeñas? Pues bien, como nuestro voto es más bien humilde, veamos el poder de \(N < P\) votos.
¿De dónde partimos? Si existe cierta incertidumbre sobre los escaños que obtendrá una candidatura, sus restos son aún menos predecibles. Por eso, consideraremos que, para una candidatura X con probabilidad de alcanzar representación, sus restos tienen igual probabilidad de estar en cualquier punto entre 0 y \(P\), sin incluir \(P\).
Bajo este supuesto, la probabilidad de que una formación con escaños, esté a N o menos de ganar un escaño es \(N/P\). Mientras que se le proyecten más de un escaño, da igual si es grande o pequeña. La misma probabilidad hay de que N votos menos le arrebaten un escaño.
Antes lo que estábamos haciendo era variar el precio, pero añadiendo votos o quitándolos no altera el precio hasta que hay un cambio. La complejidad de que pasa a partir de cuando hay un cambio en el precio, la analizaremos en otros artículos. También analizaremos la salvedad de lo que pasa cuando involucramos en el trasvase a formaciónes lejos de obtener escaño.
Resumen
Resumiendo todo lo anterior: D'Hondt es un procedimiento para buscar un precio, en votos por escaño, que reparta de forma exacta los escaños disponibles, sin que sobren ni falten. El número de votos recibidos por una formación dividido por un número de escaños da el precio máximo con el que se pueden obtener esos escaños. Esos son los coeficientes que calcula el método. Escogiendo los N mayores cocientes aseguramos que el último cociente marque un precio (\(P_{max}\)) para el que sólo se repartirán N escaños. Cualquier precio entre ese y el mayor cociente no escogido (\(P_{min}\)) serviría igualmente para obtener el reparto exacto.
Fijado un precio por escaño, todas las formaciones dedicarán sus votos a obtener escaños a ese precio y tendrán un sobrante de restos menor que dicho precio. Si tenemos incertidumbre sobre los escaños que obtendrán las candidaturas, los restos son mucho más impredecibles. Consideramos que cualquier resto es igual de probable y que el resto medio es la mitad del precio.
La existència de un precio máximo y uno mínimo sirve para analizar situaciones, por ejemplo, de trasvase de votos, ignorando lo que hacen el resto de candidaturas.
También hemos visto que, a partir de los votos a candidaturas, podemos acotar el precio entre una situación sin restos \(P_H={V_{total} \over S_{total}}\), y una situación con restos máximos \(P_L={V_{total} \over S_{total} + K }\). y que podemos estimar el precio como \(P_{E} = { V_{total} \over S_{total} + K'/2}\).
Hemos anticipado que estas cotas y estimaciones nos serviran para establecer el efecto del umbral electoral o la masa crítica de acciones de voto coordinado, por ejemplo.
D'Hondt asegura que se repartan los escaños enteros de un reparto puro proporcional (Hare). En ese sentido es bastante proporcional si hay suficientes escaños respecto al número de candidaturas con opciones. Los escaños fraccionados de Hare se reparten teniendo en cuenta los restos existentes pero también dando ventaja a las candidaturas grandes en el sentido de que cada reducción de precio, cada candidatura reduce distancia con el siguiente escaño proporcionalmente a los escaños que va a obtener.
Esta ventaja hay que relativizarla, puesto que N votos tienen el mismo poder de otorgar escaños (o quitar si se le retiran) a una candidatura grande que a una candidatura pequeña con representación.
Ahora, con todas estas herramientas en la mochila, validemos o descartemos las cosas que se dicen sobre el tema.
-
La cota superior \(P_H\) viene de que, si no hay restos,
$$V_{total} = \sum_{\forall X} V_X = \sum_{\forall X} S_X * P_H + R_X = \sum_{\forall X} S_X * P_H = S_{total} P_H$$y entonces$$P_H = { V_{total} \over S_{total}}$$↩ -
La cota inferior viene de que, si todos las candidaturas (\(K\)), tienen los restos máximos (casi \(P_L\)), entonces:
$$V_{total} = S_{total} P_L + K P_L$$y entonces$$P_L = { V_{total} \over S_{total} + K }$$Si acotamos \(P_{max}\), una candidatura ha de tener resto cero, podriamos tener una cota inferior más estricta:$$P_L = { V_{total} \over S_{total} + K - 1 }$$Por simplicidad, usamos la primera. ↩ -
La estimación supone que las candidaturas con opción tendrán, en media, la mitad de un escaño como restos. Quizás la media sería un poco más alta al incluir las que casi entran, pero estaría compensado al ignorar los restos de las muchas candidaturas que suelen quedarse lejos de la representación. En cualquier caso, la estimación suele funcionar bastante bien con pasadas convocatorias.
$$V_{total} = S_{total} P_E + K' P_E / 2 $$$$P_E = {V_{total} \over S_{total} + K' / 2 }$$↩